Tajemnica krzywej van Deemtera. Równanie van Deemtera
W poszukiwaniu złotego środka. Tajemnica krzywej van Deemtera
Rozdział mieszaniny jest jak bieg z przeszkodami. Wyobraźmy sobie mieszaninę różnych substancji, które próbują przedostać się przez kolumnę wypełnioną drobnymi ziarnami. Jedne poruszają się szybciej, inne wolniej, a naszym celem jest, aby do detektora (na metę) dotarły jako wyraźnie oddzielone grupy. W końcu chcemy otrzymać wyraźne piki, z których każdy odpowiada jeden rozdzielonej substancji.
Dlaczego jednak czasem piki na wykresie są ostre i wąskie, a innym razem rozmyte i szerokie? Odpowiedź na to pytanie daje jedno z najważniejszych równań w historii analityki: równanie van Deemtera. Jest to również chyba najbardziej popularny temat slajdu w prezentacjach przedstawicieli handlowych sprzedających kolumny chromatograficzne.
Czym jest sprawność kolumny?
Zanim przejdziemy do samej krzywej, musimy zrozumieć pojęcie HETP (Height Equivalent to a Theoretical Plate), czyli wysokość równoważną półce teoretycznej. W chromatografii im mniejsza jest wartość HETP, tym wyższa sprawność kolumny. Mówiąc prościej: chcemy, aby nasze „półki” były jak najniższe, bo wtedy na tej samej długości kolumny zmieści się ich więcej, co przełoży się na lepsze rozdzielenie składników. Uznajmy, że jedna półka teoretyczna to odpowiednik jednego małego pojedynczego podziału substancji w kolumnie. A chcemy tych podziałów uzyskać jak najwięcej.
Równanie van Deemtera opisuje zależność między parametrem HETP a prędkością przepływu fazy ruchomej. Każdy z tych trzech parametrów (A, B, C) reprezentuje inny proces fizyczny zachodzący wewnątrz kolumny. W poniższym wzorze HETP oznaczono jako H:
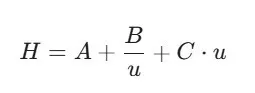
Parametry prowadzące do rozmycia pików: A, B i C
1. Czynnik A: Różnice długości pokonywanej drogi (Eddy Diffusion)
Wyobraź sobie grupę biegaczy w gęstym lesie. Każdy z nich wybiera nieco inną drogę między drzewami - jeden pobiegnie prosto, inny będzie musiał nadrobić drogi, omijając przeszkody. To samo dzieje się z cząsteczkami w kolumnie wypełnionej sorbentem.
Od czego zależy długość drogi (parametr A)? Głównie od jakości upakowania kolumny i wielkości ziaren. Lepiej w tym kontekście sprawdzają się kolumny AMT HALO z uziarnieniem wykonanym w technologii krzemionki powierzchniowo porowatej: u nas na stronie w dziale Kolumny AMT HALO
Wniosek: Im mniejsze i bardziej regularne ziarna sorbentu, tym mniejszy wpływ długości drogi A. Co istotne, ten parametr nie zależy od prędkości przepływu.
2. Czynnik B: Dyfuzja (Longitudinal Diffusion)
Cząsteczki mają naturalną tendencję do rozprzestrzeniania się z obszarów o wysokim stężeniu do tych o niskim. To klasyczne zjawisko dyfuzji. Jeśli faza ruchoma płynie bardzo wolno, cząsteczki mają dużo czasu, aby „rozpełznąć się” na boki wzdłuż kolumny, co drastycznie zwiększa szerokość piku.
Wniosek: Człon B jest szczególnie istotny przy niskich prędkościach przepływu. Im szybciej płyniemy, tym mniejszy wpływ dyfuzji na poszerzanie pików.
3. Czynnik C: Opór przenoszenia masy (Mass Transfer)
To proces „wchodzenia” i „wychodzenia” cząsteczek substancji do fazy stacjonarnej. Jeśli przepływ jest zbyt szybki, cząsteczki, które wniknęły w głąb porów sorbentu, nie zdążą z nich wyjść i dołączyć do głównego nurtu, zanim ten popłynie dalej.
Wniosek: Człon C dominuje przy wysokich prędkościach przepływu. To on sprawia, że zbyt szybka analiza kończy się rozmazanymi pikami. Czas to pieniądz ale nie zawsze da się skrócić czas analizy po prostu zwiększając prędkość przepływu fazy ruchomej
Chromatografia Gazowa (GC) vs Cieczowa (LC)
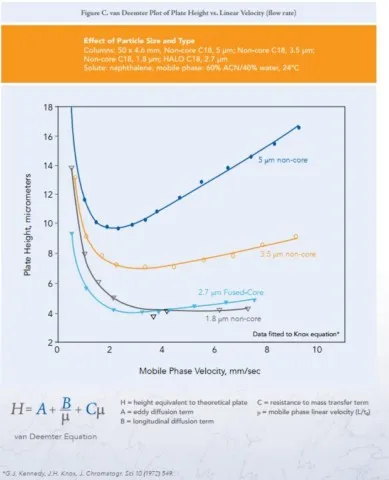
Choć samo równanie jest uniwersalne, krzywe van Deemtera dla GC i LC wyglądają nieco inaczej ze względu na różnice w fizykochemii gazów i cieczy. Przyglądając się temu tematowi, warto zerknąć na wykresy odpowiadające danej technice (cieczowej bądź gazowej). Poniżej przykład krzywej dla kolumn HPLC / UHPLC, w tym AMT HALO z ziarnem 2.7mikrona Fused Core:
Podsumowanie: optymalna rozdzielczość w chromatografii?
Krzywa van Deemtera ma kształt litery „U” (lub częściej asymetrycznej niecki). Punkt najniższy na tej krzywej wyznacza optymalną prędkość przepływu, przy której otrzymamy najwęższe piki i najlepsze rozdzielenie.
Dobierając techniki i tworząc metody analityczne dąży do tego, aby krzywa ta była jak najbardziej płaska. Dzięki temu analityk może zwiększać prędkość przepływu (skracając czas pracy), nie ryzykując, że jego wyniki nie będą optymalne. To właśnie dzięki zrozumieniu tych fizykochemicznych zależności, dzisiejsze laboratoria mogą analizować setki próbek dziennie z precyzją, o której pionierzy chromatografii mogli tylko marzyć.
Copyright Genore chromatografia © 2026